CVD 4 -Skidpad

As with the task of driving, our analysis gets a lot more complicated once we turn the steering wheel.

Analysis of longitudinal acceleration took us through thrust curve computation and into tire load sensitivity.  From this, we learned that a pair of tires produce more grip with more load, but that they produce more grip per unit load (mu) at lower loads.  Thus, one of our primary goals in setting up the car for pure cornering (or skidpad) is to keep the inside and outside tires of our the car as evenly loaded as possible.

Inside tires are far less important when performing this comparison for production cars, because they aren’t doing much.  See below, a pic from a private skidpad test day I had with the 240sx.  The inside rear tire has very little load on it:

A similar story in the front (ignore those brackets, part of a splitter I tested later)- not much weight on the inside front.  You can see the dark band where the tire has some heat in it-

There’s other things we want to do with our setup – we want to make sure our outside tires are “happy” when we are producing peak lateral grip – if they are anything less, the car won’t be able to reach its cornering potential.  This analysis assumes the cars under consideration are both equally able to make their outside tires “happy”.  There are several ways to ensure your tires are happy, and doing so is the aim of the handling and suspension tuning books.  I won’t go into any detail here to ensure your outside tires are at their best, but pictures like these, even those taken at a regular event, are a great way to validate you’ve got things working right.

But again, tuning is not the mission of this series.  The mission is to evaluate the skidpad potential of two cars, taking into consideration only their immutable physical characteristics in race trim – CG height, weight, wheelbase, track width, and maybe, wheel/tire sizes.  Like the second half of our longitudinal acceleration analysis, we aren’t going to be able to come up with any hard-and-fast numbers here.  We won’t know exactly what lateral-g our car is going to pull on the skidpad, just from crunching numbers.  There is a tuning element involved as well, and we aren’t going to know what the overall fastest balance would be here either.

What we *can* figure out, it which car is going to have its tires in better shape at a given lateral g – just as with longitudinal acceleration, we could figure out the mu needed to achieve different longitudinal accelerations.  Because in this case our inside tires will be doing some contribution, we won’t be coming up with a mu – we’ll just be looking at which car has less weight on its outside tires at a given lateral acceleration.

I’m going to state up front how our dimensions affect skidpad performance:

• Wider track width is better
• Lower CG height is better
• Shorter wheelbase is better
• Balanced static weight distribution is worth pursuing

The first two may be intuitive by now but the third may not be.  Let’s start with the easiest and most important ones first – wider track and lower CG height.

As explored previously, the amount of weight transfer our car experiences is a function of only three things – CG height, track width, and lateral acceleration.   It doesn’t matter where your roll centers are or where they went, what angles you have on your control arms, whether you have a live axle or independent suspension, whether it is AWD, RWD, FWD; it doesn’t matter what tires you have, how far the car is leaning, what hemisphere you’re in, or what you had  for breakfast.  CG height, track width, lateral accel.

We know minimizing weight transfer increased overall grip for an axle, and our goal is to produce the most lateral accel we can.

weight transfer = (weight * lateral accel * CG height)/(track width)

So to make the weight transfer number lower, we need to shrink the numerator and increase the denominator (for those that don’t remember algrebra, numerator = the stuff on the top of the fraction, denominator = the stuff on the bottom).  That means, a decrease in CG height, or an increase in track width

Sidebar – J-Rho’s Ride Height Tuning Editorial:  Getting a low CG height is very important.  In my opinion, too many people sacrifice CG height in the pursuit of other things that aren’t as important.  Take “corner weighting” for example.  Let’s say you have a car that’s at its optimally low height from a bump-handling perspective…and you want to corner weight it.  Since it is already low as it can go at all four corners, your corner weighting will only do one thing to the CG – raise it!  Often times, by a lot, 1/2″ or more.  In my experience, corner weighting just isn’t worth it if you have to raise the car higher than it would otherwise have to be.

How low should I go?  I see people concerned all the time – “but J-Rho, my lower control arms are no longer parallel to the ground” – so what?  What matters is that your outside tires are happy at terminal roll.  If your suspension starts to get bad geometry when really really low, that’s a bummer, but you should still be able to make the outside tires happy with enough static camber and caster.  Make it low, make it stiff, stiff enough that the bad geometry never has a chance to manifest.

What about bumps?  First of all, if I had a nickel for every racer who had a problem because of bumpstops, I could retire!  Throw your bump stops away (assuming doing so is legal in your class rules :))  There are only two legitimate bump stops in my mind: 1, something in the suspension (preferably the tire) hitting the chassis, or 2, the chassis hitting the ground.  “But my shocks will bottom out” – get shorter shocks!  “But my springs will coil bind” – get shorter springs!  If you *must* have bump stops, just make sure they’re only there in the last instant before the other bad bump thing happens.  I simply can’t believe how many “racers” set up their cars, drive around slow and frustrated, only later to discover they were riding on the bumpstops the whole time, and use that as some kind of reasonable excuse.  “Found out I was on the bumpstops” – well no duh!  Did you think that 1/4″ of travel was going to be enough?  Did you even look at the shock after you set the car on the ground?  It’s not like some bumpstop gnomes came out and put them there – YOU did, you are responsible for the mess.

How do I know if I’m too low?  You’re too low when your time would be faster if you were higher.  🙂  That’s kinda nebulous, so think of it this way.  If the surface you raced on were perfectly smooth, you could have the car very very low.  You would have it set so that the front suspension only reached its bump point when at or near its most extreme condition, while braking and turning simultaneously.  Similar for the rear, it would only reach that point at its extreme of turning and acceleration.  You might have it set up to rub/grind a bit even in that situation.  You have to look at the car being one of two modes – “normal” operation, and “duress” operation.  Duress would be when one or more corners of the car have gone into the bad bump state, enough that the car, at that moment, is slower than if the ride height had been set higher.   The lower you go, the faster the car will be while not in duress, but the more often it is likely to get into duress, and the greater the severity (from a time lost perspective) of the duress.  So the answer is, it is okay to hit whatever bump condition you have, but it shouldn’t be so often, or so bad, that the car would be faster on the average for the whole lap, were it raised.  The ideal ride height (and by relation, spring rate) will depend on the surface you race on – making it important to test on the same surface or one just like it.

Almost everybody I know has their car too high, or at least, don’t adequately prioritize CG height.  If my competitor has better a-arm angles, better corner weights, better working geometry, but a higher CG height, he’s going to be slower than me around the corner because he’s going to have more weight on his outside tires.

I am an especially big believer in minimizing lateral weight transfer on heavy or undertired cars.  This picture, of a modestly prepared first-gen Camaro (again, the Camaro of Liz Miles from http://www.milesspeed.com) next to a prepped ST Honda Civic, is part of what made me think the Camaro had a shot.  I was able to get the 240sx lower than the Civics, and believe I can do the same with the Camaro.

Okay, enough editorializing…

So, lowering CG height, or increasing track width, will decrease weight transfer across the car, which will increase the possible output from the tires.  These are Good Things.  Keeping more weight on our inside tires will help them do more to get the car around the corner better, will reduce the work the outside tires have to do, and especially on the driven end, will help us accelerate out of the corner and put less dependence on our limited slip.

In the next chapter, Transitions, we’ll find that width is our enemy, but here in Skidpad it is our friend.  On our example course we saw skidpad and transitions each comprised about 40% of our total time on course.  Some courses will have more, others less. Because width isn’t something we can generally adjust on our car, if our car is wider than the competition we’re looking for courses with lots of sweeping turns and few offsets; vice versa if our car is narrower.

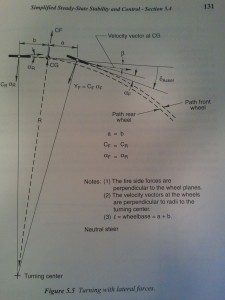
The wheelbase portion of this is not so obvious.  A diagram helps and instead of spend hours in MS Paint, I’ve gone the quick and dirty way, and snapped a photo of the relevant photo from Milliken & Milliken’s Race Car Vehicle Dynamics.  Hopefully they don’t mind me using it here – perhaps they won’t go after me for copyright violation if I can help them sell a few more copies.  The book is full of great images like this, consider picking it up!

Some things to take away from this drawing-

1, a longer wheelbase car will require more steering angle to generate the same radius turn.  In general, we don’t want to have to turn the steering wheel any more than we have to, and autocross has plenty of small-radius turns;

2, the longer the wheelbase, the larger the gap in radius between the front and rear axles, with the rear axle’s radius getting smaller and smaller as the wheelbase lengthens.  This makes the car trickier to drive “clean” and is the reason why so many drivers hit cones with the inside rear of the car – also why on the street, people run their inside rear tires up and down curbs coming in and out of driveways.  You have more vehicle to “get out of the way” before you are actually past any given element or cone.

Another thing –  a longer wheelbase vehicle, given equivalent overhangs and distribution of mass along its length, will have a higher polar moment of intertia.  While a higher polar moment is good when we are concerned about rotational stability (as we might be on a high-speed track), it comes as a detriment in autocross.  Here, we need to be able to change direction quickly, and the higher our polar moment, the more yaw (rotation of the car as seen from the top) force required to achieve a given amount of rotation.  This is compounded by #1, extra steering needed for a given radius, making the long wheelbase a double-whammy in skidpad.  Remember in skidpad, we aren’t just generating lateral force – every 1/4th of our way around, we also have to change the direction the car is heading by 90 degrees.

Static weight distribution is best if it’s somewhat near balanced front to rear.  The ideal of wide track and low CG for skidpad accomplishes one thing – it keeps the inside tires most closely loaded to the outside tires.  But what about when we twist our viewpoint 90 degrees, from a front view, to a side view, and consider the front and rear axle pairs?  Assuming equal wheel and tire sizes front to rear, we should also be trying to keep the front and rear axles as evenly loaded as possible to maximize grip – our limiting factor in skidpad performance will always be our single most heavily loaded tire.

Try as we might to minimize lateral load transfer, we can’t eliminate it completely.  However, unlike with longitudinal weight transfer in acceleration, with lateral load transfer, we can build-in some asymmetry in “roll rates”, to tweak the manner in which load is transferred from inside to outside.

For instance, if our car is naturally front-heavy (as is the case with almost every production car made),  we’re going to be worried about our outside front tire getting overloaded in our skidpad – the dreaded understeer.  We know how much total weight we are going to transfer from the inside to the outside, but we can adjust how much of that load goes across the front axle, or the rear.  In the front-heavy case, we might want to give the rear of the car more roll stiffness than the front, so that as the car builds up cornering force, more weight is transferred across the rear axle than the front.  What this does, is slow the buildup of load on the already-overloaded outside front tire, helping grip from the front axle.  That extra load instead goes to the outside rear tire, giving it an extra drop in grip efficiency, “hurting” that axle’s grip.

In the extreme case, as with a front-wheel-drive race car, you might see the rear suspension so stiff relative to the front, that the car picks the inside rear tire up completely into the air!  On rear-engined cars like the Porsche 911, it is common to see the inside front tire in the air, for similar, but opposite, reasons.

With a well-balanced car that also has good width and a low enough CG for its grip level, we get to keep all four tires on the ground.   Even though the car’s inside tires will be lightly loaded, and may be geometrically compromised, they’re still a lot more helpful to our cornering capabilities, than nothing at all.  Four tires are going to produce more grip than three, and definitely more than two!  As we’ll cover again in a later chapter on corner exit, keeping some load on the inside drive tire is going to help us a lot down the road.

…

So what do we do with this information, to tell us which car will be better around the skidpad?  Get the more important things first – CG height and track width.  CG height is a tough one to get, it’s not really published anywhere.  The government has some rollover index data but it may not cover the cars you’re examining.  Here’s a method I’ve used for approximation.

Take the height of the vehicle, subtract the ground clearance, and divide that value by two.  For instance, if subject #1 has a 54.8″ height, and 5.7″ ground clearance, our guess at CG is:

(54.8 – 5.7)/2 = (49.1)/2 = 24.55″

I usually subtract four more inches from there, so 20.55″ in this case.   Of course it’s not exact, and won’t work for all cars – convertibles, for instance, should probably drop their estimated CG another inch because they have so little above the door line.  As long as we’re consistent in our approach, and the cars we’re comparing are constructed in a similar fashion, this should work.

For width, you can use the published width value.  Usually the published value is body width, not counting side-view mirrors.   If you find a strangely wide value published for a car you’re considering, keep doing more research to ensure what you found wasn’t mirror-tip width, which might be 10″ or more wider than the body.

You can also start with the manufacturer’s or magazine-published value for front/rear weight distribution.  If you’ve done a thorough process in evaluating the car for your class, you’ll have computed the weight savings you’ll get having performed the class-legal modifications, and also noted whether that weight is coming off the front or rear axles.  Unfortunately with our production cars that start off nose-heavy, the weight we often remove (exhaust system, running low on fuel, lightweight seats) comes mostly off the rear axle too.

So let’s take a couple cars to tell which will own the skidpad – both have equal wheels and tires front and rear.

Car 1: 54.8″ factory height, 5.7″ factory ground clearance, 66.9″ width, and we’ll say it gets a BMW-esque 52% static front weight distribution.  2800 pound total weight.

Car 2: 50.5″ factory height, 4.5″ factory ground clearance, 72.3″ width, stuck with a crummy Camaro-esque 55% front weight distribution. 3000 pound total weight.

Car 1’s estimated CG height for this case is 20.55″.  Car 2’s, 19″.

###At 1g, which a good SCCA Street-Touring car should be able to do on even the worst dry asphalt surface:

weight transfer = (weight * lateral accel * CG height)/(track width)

Car 1:

X = (2800lbs. * 1 * 20.55″) /(66.9″)

X= 860 pounds of lateral weight transfer

Car 2:

Y = (3000lbs. * 1 * 19″)/(72.3″)

Y = 788 pounds of lateral weight transfer

So Car 1 started out with 1400 pounds on its left and right side, and ends up with 2260 pounds on its outside tires, only 540 pounds on its inside.

Car 2 started with 1500 pounds on each side, ends with 2288 on its outside tires, 712 pounds to give its inside tires.

At this level, both cars have a similar amount of total weight on their outside tires.  Neither car really has an advantage, and the skidpad win will have more to do with how the setup is compromised for other functions.

###At 1.2g, a good SCCA Street-Touring car should be able to do this on decent concrete:

We can skip some calcs, and see that the total weight transfer will be 20% higher than before.

Car 1: 1032 pounds transfer

Car 2: 945 pounds transfer

At 1.2g, Car 1 has only 358 pounds left on its inside tires, vs. the 2432 on its outside.  Car 2 has 2445 on its outside, 555 on its inside.

Car 1’s inside tires are getting light at this point.  It started with 52% of its weight up front (2800*.52) =  1456 pounds front, 1344 rear. 728 each front corner, 672 each rear corner.  If Car 1 was distributing the lateral load evenly between front and rear axle pairs, then each pair sees 1032/2 = 516 pounds of weight transfer.

If this is a right-hand corner, it means Car 1’s tire loadings look like this:

LF: (728 + 516)=1244      RF: (728-516)=212

LR: (672+516)=1188        RR: (672-516)=156

That 156 on the inside rear is going to be a problem for a lot of limited slip differentials.  A torsen gear-type might spin up that tire, as would a clutch-type with insufficient preload.   Car 1 could work around this a bit by increasing the lateral load transfer distribution so the front of the car transfers an extra 212 pounds, completely unloading the inside front at this level (1.2g).  That means the rear transfers 212 pounds less than before, so overall loadings would look like this:

LF: (728 + 516 + 212) = 1456     RF: (728 – 516 – 212) = 0

LR: (672 + 516 – 212)  = 976      RR: (672 -516 + 212) = 368

That’s much better from an acceleration perspective, but now we need to be worried about understeer, as the car is effectively 3-wheeling.  We need to keep in mind that we must continually be putting energy into the system just to hold a constant speed around the skidpad.  Just holding speed will require a good amount of throttle to overcome the drag created by the lateral forces, and to enable the rotation needed.

Let’s look at Car 2 at 1.2g.  It starts with 1650 on its front tires, 1350 on the rears.  825 per front corner, 675 per rear corner. 945 pounds weight transfer (we’ll round up to 950).  With even LLTD (lateral load transfer distribution):

LF: (825 + 475) = 1300     RF: (825 – 475) = 350

LR: (675 + 475) =1150      RR: (675 – 475) = 200

Similar problem here, not much weight on the inside rear.  Instead of going for complete unweighting of the inside front though, we can stiffen the front up about half that amount –  let’s say we move 150 pounds of the load transfer to the front:

LF: (825 + 475 + 150) = 1450    RF: (825 – 475 – 150) = 200

LR: (675 + 475 -150) = 1000  RR: (675 – 475 + 150) = 350

Car 2, despite its inferior front weight distribution and higher total weight, is looking better here compared to Car 1.  Both cars have their outside front tire about equally loaded, but Car 2 still has 200 pounds on the inside front tire, which will be scratching and clawing along the ground for some extra front grip.  Remember, the “grip efficiency” of a tire goes down, as its load increases.  If Car 1 is max’d out in front grip at this point, Car 2 will still have something left.  This is because Car 1, with all its front weight on its outside front tire, would be producing an efficiency of “1.2 g/lb.” (1450 pounds of load producing enough grip to laterally accelerate 1450 pounds at 1.2g)   So Car 2’s outside front tire will also be producing that same efficiency  (1450 pounds load, enough lateral force to accelerate 1450 pounds laterally at 1.2g), and the same amount of lateral grip – but – it has 200 pounds on that inside tire, which will be able to produce MORE force than is needed to laterally accelerate 200 pounds at 1.2g.  That lighter-loaded inside tire will be enjoying an efficiency *higher* than 1.2g/lb., because the efficiency goes up as load goes down; that inside tire is going to be capable of more than 1.2g/lb., so Car 2 will have more potential front grip than Car 1.

###1.45g is sometimes briefly attainable by Street Touring cars on grippy rubbered-in concrete.  How do things look then?

Car 1, 1247 pounds load transfer

Car 2, 1142  pounds.

At this point the narrower Car 1 is really fighting for drive traction.  It likely lifted its inside front tire a while ago, with all additional weight transfer over 1.2 coming off the inside rear tire.

LF:  (728 + 728) = 1456     RF: (728 – 728) = 0

LR: (672 + 519) = 1191       RR: (672 – 519) = 153

Car 1 is close to bicycling with the slightest bump or additional lateral disturbance.  Better hope it has a good diff!

Car 2 is a bit better off.  There’s still some flexibility in tuning, depending on how the outside front tire takes to the additional load.  If it takes it well, it could go for complete unloading here:

LF: (825 + 825) = 1650    RF: (825 – 825) = 0

LR: (672 +  317) = 989     RR: (672 – 317) = 355

So, if the outside front can do it, Car 2 could keep the same inside drive tire loading at 1.4g, Car 1 had at 1.2g.  If the car pushes too much, there’s room to transfer 150-200 pounds to the inside front tire, while still keeping the inside rear tire just as loaded as Car 1’s.

################

The point of this analysis is to show how lower CG and wider track can make up for more weight and/or inferior static weight distribution.  For cars of similar starting weight and distribution, the advantage would be even more apparent.  Higher CG and narrower track reduce one’s ability to tune the car’s handling balance at high grip levels – at some point the car is going to pick up inside wheels and there’s nothing you can really do to prevent it once the car is as low as it’s going to get.  A car that has an advantage with four tires, will likely be at a disadvantage once one goes airborne.

Narrow car fans, don’t worry though, the width will come back to bite the big car in the next chapter, Transitions.

Wheelbase is difficult to factor in because its effects are dependent on corner radius – the larger the radius, the less impact it has.  Leave it as a standalone variable to consider last – if two cars are very similar in skidpad potential at the grip levels you’re likely to encounter, the advantage goes to the shorter wheelbase car.