CVD 3b -Rolling Accel (complex)

There’s a lot of nonsense out there, in the previous chapter bit we hopefully armed you with the tools to enter any “hp vs tq” battle and come out victorious.

One other area where I see some nonsense, is in mis-quoting important people’s famous quotes.  One of them is Mark Donohue’s quote from his journey in developing the Porsche 917-30, pertaining to power and how much was enough:

The first time I drove the car with the motor working the way it should, I came in and said, “Boy, this is one strong mother!”  None of the Germans  were familiar with the term, so I had to explain that it meant “very, very powerful.”  From then on they used the expression quite a bit without knowing its real derivation.  They asked me if it had enough power then and I said, “No.  It will never have enough power until I can spin the wheels at the end of the straightaway in high gear.”  They were aghast at that.  They had never seen motors put out even as much power as we had.  As they reached 800 horsepower, they literally burned out one of their dynamometers.  By the end of the year the five-liter engine was up to 880 horsepower, and the best 5.4 liter engine in 1973 was eventually good for 1190 horsepower.  All the time they kept asking, “Now does it have enough?”  And I kept saying, “I still can’t spin the wheels all the way down the straightaway.”

So the next time the question comes up – do I have too much power, or could I use more?  That’s the test – can you overwhelm your tires even in a lowest-thrust situation, usually the highest speed and highest gear you’ll see?  If so, then you have enough.  It’s really really rare for someone to have more power than they need, even in autocross, where the speeds are very low, the surfaces aren’t as good, and the opportunities to drive straight limited.  In this, the latter half of the rolling acceleration chapter, we’ll help you figure out when you have enough horsepower.

There’s a corollary to what we’ll call “Donohue’s law of power”.  Namely, when do I have enough grip?  It’s the opposite answer – you don’t have enough grip until you can drive a whole lap at full throttle.  Unfortunately in chasing this goal, production cars will want to tip over when the grip levels get very high.  So at least, until your limiting factor is the shiny side not staying up, you don’t have enough grip.

We’ve examined how our engine, gears, and tires work together to accelerate the car.  At the end, a bomb was dropped – our maximum acceleration might be limited by our grip.  If the cars we’re considering are all very low powered, then maybe wheelspin isn’t a concern.  But if the power levels are high enough, an examination of the cars’ relative ability to “put power down” warrants consideration.

In order to explain what limits this ability, we have to talk about tires.  Tires are hugely important.  A simple change in tires can catapault a car ahead of its competition, drop seconds off lap times with no other changes, and win a championship.  No comparison between two cars has any validity unless you know they type and condition of the tires on each car.  Do not underestimate the importance of tires to the overall performance of the vehicle!

Our car’s four contact patches, each not much bigger than your hand, are the only means we have to take everything we produce, and turn it into something that makes the car move.  Everything we do with the chassis and suspension, is done with the goal of getting more out of those four little critters.

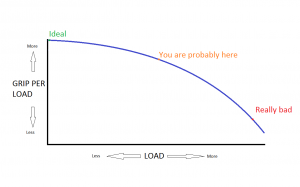
The following graph explains the most important thing you need to know about all tires on all production cars.  Since it is so important a concept, I’ll state it a few different ways, hopefully one of them clicks and makes sense with the reader.  Nothing in any of the chapters to follow, will make any sense until you get this, a slightly exaggerated tire load response curve:

Most succinctly, as we increase the load on a tire, the total grip the tire provides goes up, but the amount of grip we get per unit of load (this is also known as coefficient of friction, or “mu“), goes down.  The more we increase load, the greater the rate of grip drop-off; it just gets worse and worse.  On the other side, as we decrease load, we lose grip, but we don’t gain as much mu from the load decrease, as we lose from an equal load increase.

Picture a car with 50/50 front:rear weight distribution.  This car also happens to have 50:50 left:right weight distribution.  To many this is a “perfectly balanced”* car.  It also has equal sized wheels and tires at all four corners.  Oh, and it’s all-wheel drive with a 50:50 front/rear torque split.

*50/50 static weight distribution is nowhere near ideal for practically everybody – we’ll cover why later

This car will *NEVER* produce as much grip, as it does when at rest (or at least, not accelerating).  As soon as this car begins turning, weight will shift from the inside tires to the outside tires – the outside tires will be able to produce more total grip because of the increase in load, but the inside tires will lose more of their ability to produce load, than the outsides gained.  Net result – a reduction in total grip.  Same goes for acceleration (remember this car is AWD) – as soon as we accelerate, weight transfers from the front axle to the rear, because while the rear axle will gain grip producing ability from the weight transfer, it will not gain as much as the front loses; again, a net loss in total grip available.

Whether you’re looking at front vs. rear, or left vs. right, the optimum grip situation (considering the above car with balanced and equal static weights and tires) will be when both sides are equally loaded.

The lighter loaded, the better.  Reducing total vehicle weight moves all four tires “left” on the curve, towards a more ideal situation, because each tire has less load.

Putting bigger, or better, tires on the car,  assuming equally good wheel width support, will produce a new curve, up above the existing one.  The same load on a bigger/better tire will give you more mu, and/or put you at a more favorable spot on its load response curve.

For many where this clicks is in the things we do in tuning our car’s cornering balance with springs, swaybars, and even shocks..  If we stiffen our front springs or front swaybars, while leaving the rear alone, then when our car is in a corner, we are going to cause *more* weight to transfer from the inside front tire, to the outside front tire at a given cornering acceleration.  This is going to *increase* the load difference between our two front tires, reducing the total grip available from those tires, relative to the rear.  In this example, by increasing the load transfer at the front tires will reduce the load transfer at the rear tires, adding grip to the rear.  Overall, this will tend to shift the balance of the car to understeer, where the front tires lose grip first.  If this has clicked, it’s easy to see why – it’s because we reduced their grip capacity by increasing their load differential!

I’m not a very good teacher and can’t think of any more ways to explain this.  If it’s not clicking for you yet, you can try letting it sink in for a while, reading it again, or checking out some of the books I’ve listed previously.  They all contain a section on tires, that covers this principle.  It is the core of everything we do to make our cars handle better.

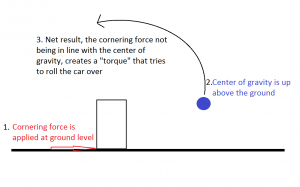
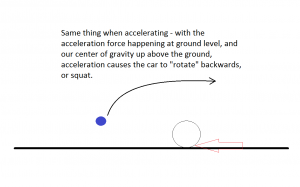
A common misconception is that the amount of roll a car produces, or the amount it squats, is somehow indicative of the total load transfer.  This is not at all true.  Load transfer is a function of only three things – how far apart the tires are, how high the CG (Center of Gravity) is, and how much acceleration is being produced.  Here are a couple illustrations showing just one tire, and a blue circle illustrating the CG’s location.  My drawing skills are severely feeble so please just try to picture the rest filled in with your favorite car.

In this one, we are looking at the back of the car as it is going around a right-hand corner.  The tire could be a front or rear tire:

In this illustration, we are looking at the left side of a rear-wheel drive car, as it is accelerating forward from right to left:

So again, it doesn’t matter what suspension type we have, what suspension geometry we have, where our roll centers started or where they went, how much the car is visibly rolling or squatting, whether one is an M3 and the other is a Pinto – if two cars have the same track width (for lateral weight transfer), wheelbase (for longitudinal weight transfer), and CG location, they will transfer the EXACT SAME load for a given acceleration.  Some funny things happen when our car starts to pick tires up off the ground but for the most part, remember the above.

Unfortunately, unlike our study of theoretical acceleration previously, we are not going to be able to produce any sort of absolute numbers out of this exercise, or really, any of the other exercises going forward.  This does not mean we cannot perform meaningful comparisons.  What we can do, is look at the cars under consideration, in various states, and compare how things look, from the perspective of their tires, in those states.  As illustrated by the tire load response curve above, the car with the tires “better” loaded (“better” will be different things in different situations) will have the capability to produce more grip, and should be faster.  To reiterate something mentioned in the intro chapter, we’re basing this on a few assumptions, a big one of which is that we can do what is necessary to make the harder-working tires, equally “happy”, from an alignment perspective, when in their maximum state.  This may seem like a far-fetched basis when comparing cars of varying suspension types but as we’ll cover later it’s not as bad as you may think.

So, not to sidetrack the discussion too much with cornering considerations, our focus for the moment is rolling pure longitudinal acceleration.  If we have two cars, on the same tires, which one will have the greater potential for longitudinal acceleration?

I am ignoring the concept of “anti-squat” for this discussion, which does play a role.  If you feel your knowledge in this area is incomplete without a thorough understanding of anti-squat, the Herb Adams book listed in the intro chapter does a great job explaining it

Longitudinal acceleration is a bit different from cornering, or lateral acceleration because for most cars, half the tires are just “along for the ride”.   In a rear wheel drive car, the front tires contribute nothing more than more work to do, in accelerating the car.  Ditto for the rear tires of a front-wheel drive car.  In an all-wheel-drive car we get to use all four tires, a big advantage, if we can take advantage of it.

Let’s now show how we quantify our weight transfer.  Let’s take a theoretical car, with a 50/50 front:rear weight distribution, total weight of 3000 pounds, a wheelbase of 100 inches, and a CG height of 20 inches.  Let’s say it is accelerating at .5g.  How much weight is transferred from the front tires to the rear tires?

Again, regardless of suspension geometry, how much we see the car squatting, and even whether its f/r/awd, we can tell how much weight is transferred from just the above info.  The formula:

(Total Weight  * CG Height * acceleration)/(Wheelbase)

For a preview of the skidpad chapter, lateral weight transfer is the same, with Track Width substituted for Wheelbase)

So, plugging in the numbers for our theoretical car:

(3000lbs. * 20″ * .5)/(100″)

(30,000lbs.-in)/(100in)

300 pounds of weight transfer

So the car started off with 1500 pounds on the front tires, and 1500 pounds on the rear.  As it accelerates at .5g, it now has only 1200 pounds of load on the front tires, and 1800 pounds on the rear – a 20% increase!  Now, that won’t create anywhere near a 20% increase in available acceleration grip, but it will be a good increase nonetheless.

What happens if we shorten the car’s wheelbase by 10″, to 90″?

(3000lbs. * 20″ * .5)/(90″) =  333.3 pounds of weight transfer, about 10% more than before, granting 1833.3 pounds on the rear tires, a 22.2% increase.

Notice how the % increase in rear wheel loading, is the same as the CG height divided by the wheelbase?

It is not inconceivable, with enough power, grip, and/or high enough CG, that we might transfer all weight to the rear tires when accelerating.

This is a good time to point out the basic reason why rear wheel drive is better than front wheel drive for racing.  In racing, we need the car to accelerate.  Accelerating moves load from the front tires to the rear.  In a rear drive car this is beneficial, because the act of accelerating, creates a positive feedback, giving the rear tires more grip, with which to provide more acceleration.  The opposite happens on a front wheel drive car – as it accelerates, load still transfers rearward, but that’s away from the front tires, which have to do all the work in accelerating the car, and the better the job they do, the less total grip they get to try to continue doing it with.

All-wheel drive vehicles are a tricky thing.  By their nature, they always have all their load on their drive tires.  A lot of the wizardry in making an AWD car really accelerate well, is managing how power is sent to the differentials.  You want the power sent in a way that maps to the load on the tires.  At rest, you’d want a torque split that mimics the car’s static weight distribution (let’s say 60 front, 40 rear for something like a Mitsubishi Evo).  As the car begins to accelerate harder, it might make sense to shift to 50:50, as some load transfers to the rear, and as the car reaches its peak acceleration (likely limited by the engine’s output!), it might be best to send over 50% to the rear wheels.  This is just from a pure-acceleration perspective, not taking into account cornering considerations.

So based on the formula for weight transfer, we can figure a few things.   “Better” here does not mean “better” overall – only as it applies to comparisons of longitudinal accelerative capability:

• For a rear-drive car, a greater portion of the static weight on the rear tires is better
• For a rear-drive car, a shorter wheelbase is better
• For a rear-drive car, a higher CG height is better
• For a front-drive car, a greater portion of the static weight on the front tires is better
• For a front-drive car, a longer wheelbase is better
• For a front-drive car, a lower CG height is better
• For an all-wheel-drive car, optimal static weight produces 50/50 front:rear weight distribution, at the thrust value where all four tires break loose
• For an all-wheel-drive car, we need to manage our diffs in line with our CG height, wheelbase, and acceleration

		Front-wheel-drive drag cars are built to have a very low CG height, a very front-biased static weight distribution, and use wheelie bars to artificially extend their wheelbase – in combination, they are able to achieve impressive results on the dragstrip.

---

…

We’re nearing a point where we’ll be able to perform a more complete analysis of longitudinal accelerative capability between two cars.  We know which one is stronger based on its engine, gearing, tires, weight.  But we don’t know which one will be better able to put down that power.  For most cars in most cases, this won’t be an issue, as we won’t have enough power to spin the tires from a roll.  But as power levels rise or grip levels go down, this may come into play.

The general theme is a car with more weight (statically and dynamically) over its drive tires, will have a higher ceiling of potential acceleration.  Let’s do an example.  Three cars, all 3000 pounds, all with the same wheels/tires at all four corners, all 60% front weight distribution, 100″ wheelbase, and 20″ CG height.

One is FWD, one, RWD, one AWD.  Which will have the highest potential rolling acceleration?

The AWD car in all cases, of course.  Sure, if you totally borked the thrust management in the diffs you could make it just as bad as whichever other one was worse at that time, but you’d have to try pretty hard to do so.

So how about between the FWD and RWD car?  For that, it depends on how hard we’re accelerating, which itself is limited by the tires, the surface, conditions, etc.

At .25g (very light) acceleration, we have (3000 * 20 * .25)/100 = 150 pounds of rearward weight transfer.  So both cars went from 1800lbs. (60% of 3000) to 1650lbs on their front tires.  So at this point, the FWD car has 1650lbs. on its drive tires, while the RWD car only has 1350.  To achieve this acceleration, the FWD car’s tires are going to need a coefficient of friction, or mu, of (3000*.25)/1650 = 750/1650 = .45.  The RWD car’s tires would have to have a mu of (3000 * .25)/1350 = 750/1350=.55.  While the RWD car’s tires are more lightly loaded and thus in a “happier” point along the tire load response curve, it is not likely the mu is 20% better.  If we are not accelerating very hard, then our 60% front-weight car will need a lower mu in FWD form.

At .5g (modest) acceleration, we have (3000 * 20 * .5)/100 = 300 pounds of weight transfer.  At this rate, our car is at a dynamic 50/50 front:rear weight distribution (1500 front and rear).  The FWD and RWD car have equal amounts of weight on the drive tires.  Past this point in acceleration, the RWD car will have better acceleration grip, and that advantage only increases as the acceleration continues to increase.  Either car needs an effective mu of (3000 * .5)/1500 = 1.  This should be perfectly achievable with a decent tire on a decent surface, but may not be possible in the wet.

At .75g (strong) acceleration, we have (3000 * 20 * .75)/100 = 450 pounds of weight transfer.  1350 (45%) on the front tires, 1650 on the rears.  It is not very likely the FWD car has sticky enough front tires to accelerate at this rate.  Doing so would require a tire mu of (3000 *.75)/1350 = 2250/1350 = 1.66!  Not very likely in most cases, maybe with the stickiest slicks out there.  Meanwhile the RWD car would only require a mu of 2250/1650 = 1.36, a bit more achievable.

At 1g (very strong) acceleration, (3000 * 20 * 1)/100 = 600 pounds of weight transfer.  Fronts are light with only 1200lbs. load, rears are up to 1800.  Dynamically, the car has gone from 60% of the load on the front tires, to 60% of the load on the rear tires.  RWD car needs a mu of (3000 * 1)/1800 = 1.66, same as our FWD car needed to to .75g; this thing is going to need slicks to actually pull that number.

For the AWD car to do 1g, it needs an average mu from all four of its tires of just 1!  That’s because all of its weight is on its drive tires, it gets (3000 * 1)/3000.  The tricky part, as mentioned above, will be ensuring the diffs apportion the output to the tires with the load, to keep from spinning one pair too soon.

So that example was for a car with 60% front weight distribution.  For a RWD car, that is really really poor – even the worst Mustangs manage only high 50’s.  Let’s show the difference having a more beneficial different static weight distribution has-

Let’s say the car is built at 50/50 front:rear weight distribution, and wants to do .75g (which is a good strong 2nd gear acceleration for a moderately powerful car) acceleration.  It still transfers 450 pounds rearward, but since it started at 1500/1500, it now has 1950lbs. on the rear tires.  Effective mu needed = (3000 * .75)/1950 = 1.15, which is plenty reasonable.

The Porsche 911 is much maligned for its ancient rear-drive layout – but how does that configuration affect its ability in rolling acceleration?  Let’s say our theoretical test car was based with the same 60% static rear weight distribution.  At .75g it will have 2250lbs. on the rear tires, needing only a mu of 1 to maintain traction – the same place our 60/40 car was at .5g.

We’ve seen here how having over 50% static rear weight distribution has a positive affect on longitudinal grip for a RWD car – we’ll also see later why it’s not necessarily terrible for handling too.  And if >50% rear is better for accelerating and handling, maybe 50/50 shouldn’t be our target after all.

…

In conclusion, unlike part 3a where we were able to put a precise (if theoretical) number on our car’s acceleration, in this case, we can only work to predict the mu needed to achieve a certain acceleration for a given car.  The way we use this in comparison, is to know that a car needing higher mu values to achieve a given acceleration value, is going to be more dependent on having stickier tires or good surface conditions.  As we’ll also see later, a tire can only do so much at one time, so if the car is able to easily deal-out the grip needed to accommodate accelerative needs, it means there may be more grip left over to handle the cornering needs.

There aren’t any hard-and-fast rules on what tires or conditions produce different mus – but you might figure <1 for a normal 2011 street tire, 1.1-1.2 for a top-of-the-line “extreme summer performance” 140-200 treadwear street tire, as used in the SCCA’s Street Touring classes, 1.3-1.4 for a Hoosier or Kumho DOT-approved R-compound tire, and 1.5+ for a full-on non-DOT slick.  This is assuming fresh tires, in their prime operating range, on a quality surface.  Rain, dirt, cold temps, and a whole lot of other factors can decrease this.  The tire pressure that’s ideal for longitudinal grip, may not be ideal for handling, so a compromise between the two must be struck.